§5.3
微积分基本公式
一、积分上限的函数及其导数
设函数![]() 在区间
在区间![]() 上连续,并设
上连续,并设![]() 为
为![]() 上的一点,考察
上的一点,考察![]() 在部分区间
在部分区间![]() 上的积分
上的积分
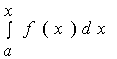
这一特殊形式的积分有两点应该注意:
其一、因![]() 在
在![]() 连续,该定积分存在。此时,变量
连续,该定积分存在。此时,变量![]() “ 身兼两职 ”,既是积分变量,又是积分的上限。
“ 身兼两职 ”,既是积分变量,又是积分的上限。
为了明确起见,将积分变量改用其它符号如![]() 来表示,这是因为定积分与积分变量的选取无关。上面的定积分改写成下述形式
来表示,这是因为定积分与积分变量的选取无关。上面的定积分改写成下述形式
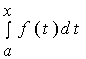
其二、若上限![]() 在
在![]() 上任意变动,则对应于每一个取定
上任意变动,则对应于每一个取定![]() ,该定积分有一个对应值。所以,它在
,该定积分有一个对应值。所以,它在![]() 上定义了一个新的函数, 记作
上定义了一个新的函数, 记作![]()
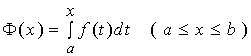
称![]() 为以积分上限为变量的函数( 简称变上限函数 )。
为以积分上限为变量的函数( 简称变上限函数 )。
是否确有这类函数?
观察一个例子,正态曲线![]() 在
在![]() 上的变上限函数为
上的变上限函数为

它表示一个曲边梯形的面积。运行程序gs0503.m,可分别作出![]() ,
,![]() 在
在![]() 上的图象
上的图象

这表明,![]() 确实是一个新的函数。
确实是一个新的函数。
【定理一】如果函数![]() 在区间
在区间![]() 上连续, 则变上限函数
上连续, 则变上限函数
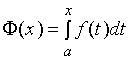
在![]() 上具有导数,且它的导数是
上具有导数,且它的导数是

证明:当上限![]() 获得增量
获得增量![]() 时,
时, ![]() 在
在![]() 处的函数值为
处的函数值为
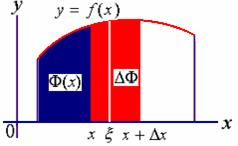
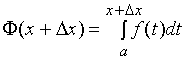
由此得函数的增量
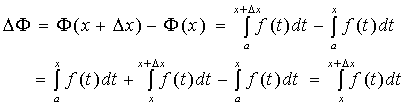
据积分中值定理:
![]()
![]() 在
在![]() 与
与![]() 之间
之间
![]()
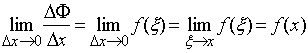
即:
![]()
定理一表明:![]() 是
是![]() 的一个原函数。因此,我们便有下面原函数的存在性定理。
的一个原函数。因此,我们便有下面原函数的存在性定理。
【定理二】如果函数![]() 在区间
在区间![]() 上连续, 则函数
上连续, 则函数
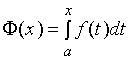
就是![]() 在
在![]() 上的一个原函数。
上的一个原函数。
定理二的重要意义在于:
其一、肯定了连续函数的原函数的存在性。
其二、揭示了定积分与原函数之间的联系。 使得定积分的计算有可能通过原函数来实现。
二、牛顿-莱布尼兹公式
【定理三】设![]() 在
在![]() 上连续,
上连续, ![]() 是
是![]() 在
在![]() 上的任一原函数
上的任一原函数
则 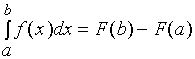
证明:![]() 与
与![]() 均是
均是![]() 在
在![]() 上的原函数
上的原函数
则 ![]() (
( ![]() 为常数,
为常数, ![]() )
)
令 ![]() ,
, ![]()
而
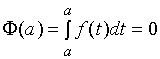
故
![]()
从而
![]()
即
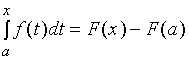
若令![]() , 得:
, 得: 
为了方便,今后记![]() 或
或 ![]() 。
。

最后,我们提醒一句,微积分基本公式时,一定要注意条件:
![]() 是
是![]() 在区间
在区间![]() 上的原函数。
上的原函数。
【例1】计算 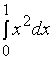 与
与 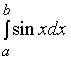
解: 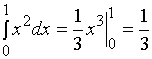
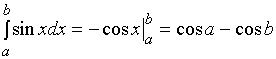
注:当初阿基米德用穷竭法计算定积分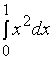 ,可是费了不少功夫,可如今变得简单多了,这得益于微积分基本公式。
,可是费了不少功夫,可如今变得简单多了,这得益于微积分基本公式。
【例2】设![]() 在
在![]() 内连续,且
内连续,且![]() ,证明函数
,证明函数
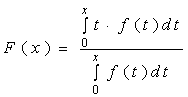
在![]() 内为单调增加函数。
内为单调增加函数。
证明:

由假设,
在![]() 上
上 ![]() ,
, ![]() , 故
, 故
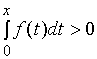 ,
,  ,
,
![]()
从而,
![]() 在
在 ![]() 上是单增的。
上是单增的。
【例3】求极限 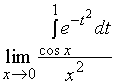
解:这是一个![]() 型的不定式,可用罗必达法则来计算,分子可写成
型的不定式,可用罗必达法则来计算,分子可写成
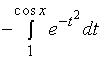
它是以![]() 为上限的函数, 作为
为上限的函数, 作为![]() 的函数, 它可视作以
的函数, 它可视作以![]() 为中间变量的复合函数, 故
为中间变量的复合函数, 故
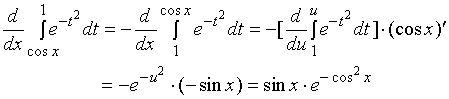

注明:试图用牛顿 -- 莱布尼兹公式计算定积分的思路是不可取的。这是因为![]() 不具有有限形式的原函数。
不具有有限形式的原函数。

公元前的古希腊数学家阿基米德最先具有定积分的初步思想方法,而明确提出定积分概念却是由牛顿(英1642 - 1727)与莱布尼兹(德1646-1716)共同完成的。 而当时的定积分理论基础尚不严谨, 甚至连个严格的定义都没有。直到(1826 - 1866)德国数学家黎曼给出了今天的定积分严格定义。
这一事实表明:一个科学概念从萌芽、诞生到成熟需要经历很长时间。 因此,列宁称“
自然科学的生命是概念 ”再恰当不过了。
定积分的符号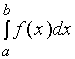 是由莱布尼兹首先引用的。其含义是:定积分的实质是求积分和式的极限,英文中求和一词是Sum,将S拉长变成了
是由莱布尼兹首先引用的。其含义是:定积分的实质是求积分和式的极限,英文中求和一词是Sum,将S拉长变成了![]() 。显然,符号
。显然,符号![]() 从外形到含义均表达了“求和”的涵义,堪称“形意兼备”。莱布尼兹在微积分中引用的符号系统:
从外形到含义均表达了“求和”的涵义,堪称“形意兼备”。莱布尼兹在微积分中引用的符号系统:
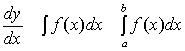
彼此之间有联系,又各自表达不同的意义,可以说十分先进。现代计算机数学软件所采用的符号系统便是莱布尼兹所定义的,由这一点可看出先进的符号体系是重要的。
我国古代数学尽管历史悠久,但发展缓慢,其中一个重要的原因是符号落后。象著名的“勾股定理”也仅被表述成:勾三股四弦五,即:
![]()
在计算机编程中,合理有效地使用符号与变量的名称更是一个不容忽视的大问题。